函数 (1)

主要内容包括:

集合与简易逻辑
函数的概念与基本性质(抽象函数的基础)
基本初等函数(模型)
应用

解题中很多基础作为前置知识, 比如代数方面, 平方根, 二次方程等.

1. 集合与简易逻辑

1.1 集合

集合的概念, 元素的概念. 以及集合与元素的关系 (属于 $\in$ 和不属于 $\notin$ ).
集合通常用大写字母表示, 元素通常用小写字母表示.
集合的三个特征: 确定性, 互异性, 无序性. (这是中学阶段解题的一个关键, 常用与分类讨论的依据).
集合的类型: 有限集, 无限集, 空集 ( $\empty$ ).
集合的表示方法:
- 列举法. 一个各个枚举出来.
- 描述法. 使用表达式与逻辑符号描述.
几个特殊集合: 自然数集 $N$ , 正整数集 $N^{*}$ 或 $N_{+}$ , 整数集 $Z$ , 有理数集 $Q$ , 实数集 $R$ , 复数集 $C$ .

特殊集合的符号一般使用双线大写, 但不同习惯描述不同.

几点注解:

属于和不属于是元素与集合的关系 (集合与集合的关系是包含 $\subset$ ).
空集是一个集合.
$a$ 与 ${a}$ 的含义是不同的. ${0}$ 和 $\empty$ 也是不同的.
无限集只能使用描述法.

关于一些题型的说明:

区分集合与元素的概念, 元素与集合的关系, 用 $\in$ 或 $\notin$ 来填写一些关系. 通常进阶是使用方程等一些具有多个解集的问题来提升难度. 综合上需要运用多个常识性问题, 例如不等式, 绝对值, 平方根下为非负数等. 中学阶段以实数系为参考, 多半不会参考虚数单位. 另外就是强调确定性, 出现模棱两可的不在判断的范围, 比如高个子的组成的集合等.
另一种则是利用无序性和互异性来做文章. 给定一些方程, 或有多个解的表达式, 然后描述两个集合的关系, 在无法确定的情况下, 需要分类组合进行讨论, 给出解答.

老龙门的例题还是很经典的.

1.2 子集, 交集, 并集, 补集

集合关系的描述: $\subset$ , $\subseteq$ , $\cup$ , $\cap$ .
补集会在一个基础范围内讨论, 通常会被称为全集, 常用 $I$ 或 $E$ 表示, 集合 $A$ 的补集写成 $C_{E} A$ . 为了简化也会将全集省略, 写成 $C A$ .
韦恩 (Venn) 图描述法.
中学阶段常常会重点强调子集, 真子集的概念. 这也是常常出题的地方.

关于一些题型的说明:

添加集合与集合的关系后, 结合元素与集合的关系, 这两个是经常会被混淆的概念, 作为基础题型经常出现.
在就是关于包含关系的隐含条件. 例如 $A \cap B = A \Rightarrow A \subset B$ .
这里经常出现需要分类讨论的题型.

1.3 简易逻辑

可以判断真假的叫命题.
"或", "且", "非" 是逻辑连词. 不含逻辑连词的命题是简单命题. 含有逻辑连词的命题是复合命题.
四种命题 (这是逻辑的核心基础).
- 原命题
- 否命题
- 逆命题
- 逆否命题
四种命题的关系:
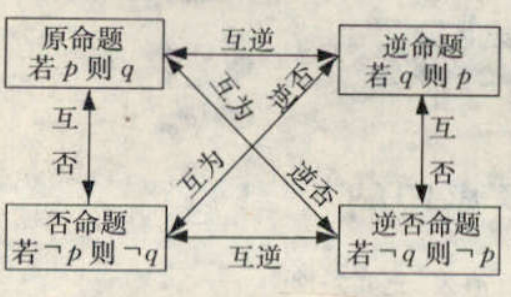
真值表 (或, 且, 非).
充要条件 (重点)
- 若 $p \Rightarrow q$ , 则 $p$ 是 $q$ 的充分条件. $q$ 是 $p$ 的必要条件.
- 如果 $p \Rightarrow q$ 并且 $q \Rightarrow p$ , 则 $p \Leftrightarrow q$ , 即 $p$ 是 $q$ 的充分条件, $p$ 也是 $q$ 的必要条件, 被称为充分必要条件, 简称为充要条件. 事实上这时 $p$ 与 $q$ 等价.

2. 函数的概念

2.1 函数的概念

函数的定义
- 函数古典定义. 采用变化的观点, 使用对应法则来定义函数. 观点中因变量 $y$ 是自变量 $x$ 的函数. 没有集合的概念引入.
- 函数的现代定义. 现代映射的观点, 集合论的描述方式.
- 一些概念: 定义域, 值域, 映射, 对应法则. 象, 原象.
- 函数相等的判断有两条: 定义域和对应法则. 这是中学阶段出题的一个隐藏点.
图像的定义. 采用集合的语言: $G := {(x, y) | f (x, y) = 0}$ .
函数的表示法: 表格法, 图像法, 解析式法.
复合函数.
区间的概念.

需要注意的是函数值必须唯一存在.

2.2 函数的三要素

三要素: 定义域, 值域, 对应法则.

求定义域, 值域等, 包括函数表达式的变形与等价转化都是常考的题型范围.

关于解题的小结. 定义域常见求法:

若函数 $f (x)$ 是整式, 定义域是全体实数.
若函数 $f (x)$ 是分式, 要求分母不为 $0$ (实数范围).
若函数 $f (x)$ 是偶次根式, 那么定义域为被开放式为非负实数.
函数 $f (x) = x^{0}$ , 那么定义域为 $(- \infty, 0) \cap (0, + \infty)$ .
复合函数定义域需要考虑内层函数的值域要受限于外层函数定义域的条件.

2.3 函数的图像

重点是怎么绘制出图像: 描点法
函数图像的变换(重难点):
- 平移变换
- 伸缩变换
- 对称变换
- 翻转变换

1) 平移变换

将函数 $y = f (x)$ 向左平移 $h, h > 0$ , 得到函数 $y = f (x + h)$ .
将函数 $y = f (x)$ 向右平移 $h, h > 0$ , 得到函数 $y = f (x - h)$ .
将函数 $y = f (x)$ 向上平移 $k, k > 0$ , 得到函数 $y = f (x) + k$ .
将函数 $y = f (x)$ 向下平移 $k, k > 0$ , 得到函数 $y = f (x) - k$ .

总结一下平移规则:

将原来的 $x$ 或 $y$ , 变成 $x + h$ 或 $y + h$ , 其中 $h > 0$ , 就是将原来图像按照 $x$ 或 $y$ 轴的负方向移动.
将原来的 $x$ 或 $y$ , 变成 $x - k$ 或 $y - k$ , 其中 $k > 0$ , 就是将原来图像按照 $x$ 或 $y$ 轴的正方向移动.

所以平移变换可以写成:

{\begin{array}{rcl} x^{'} & = & x + a, \\ y^{'} & = & y + b \end{array}

其中 $x$ , $y$ 是原坐标, $x^{'}$ , $y^{'}$ 是新坐标, 该表达式表示将函数沿 $x$ 轴的负方向移动 $a$ 个单位, $a$ 如果为正, 则是向左移动, 若 $a$ 为负, 则相当于向右移动. 类似的向 $y$ 轴负方向移动 $b$ 个单位.

2) 伸缩变换

横向伸缩 (纵坐标不变). 将函数 $y = f (x)$ 的图像上的所有点的横坐标缩短或伸长到原来的 $1 / ω$ , 得到函数 $y = f (ω x)$ . 若 $ω > 1$ 则是缩短, 若 $ω \in (0, 1)$ , 则是伸长.
纵向伸缩(横坐标不变). 将函数 $y = f (x)$ 的图像上的所有点的纵坐标伸长或缩短到原来的 $A$ 倍后得到函数 $y = A f (x)$ . 其中若 $A > 1$ 是伸长, 若 $A \in (0, 1)$ 则是缩短.

伸缩变化的总结. 与平移变换类似:

将 $x$ 变成 $ω x$ 就是将图像的 $x$ 坐标变成原来的 $1 / ω$ . 若 $ω > 1$ 就是缩短, 若 $ω \in (0, 1)$ 就是拉伸.
将 $y$ 变成 $1 / A$ , 实际上 $A \neq 0$ , 放在表达式右侧, 移到左边就是 $1 / A$ , 可以将其记为 $σ$ . 也就是将 $y$ 变成 $σ y$ 就是将图像的 $y$ 坐标变成原来的 $1 / σ$ . 若 $σ > 1$ 就是缩短, 若 $σ \in (0, 1)$ 就是拉伸.

所以伸缩变换可以写成:

{\begin{array}{rcl} x^{'} & = & ω x, \\ y^{'} & = & σ y \end{array}

其中 $x$ , $y$ 是原坐标, $x^{'}$ , $y^{'}$ 是新坐标, 它表示将原来函数图像的所有横坐标变成原来的 $1 / ω$ , 将原来函数图像的纵坐标变为原来的 $1 / σ$ .

3) 对称变换

函数 $y = f (x)$ 的图像与函数 $y = - f (x)$ , $y = f (- x)$ , $y = - f (- x)$ 的图像分别关于 $x$ 轴, $y$ 轴, 和原点对称. 本质上依旧是变换:

沿 $x$ 轴对称就是 $x^{'} = - x$ .
沿 $y$ 轴对称就是 $y^{'} = - y$ .

4) 翻转变换

将函数 $y = f (x)$ 的图像在 $x$ 轴上方的部分不变, 将下方的部分翻转到上方, 得到函数 $y = | f (x) |$ .
将函数 $y = f (x)$ 的图像保持 $y$ 轴右侧的不变, 将左侧翻转到右侧, 得到函数 $y = f (| x |)$ .

3. 函数的性质

3.1 函数的单调性

单调性的定义.
相关概念: 单调区间, 增函数, 减函数.

有关结论:

若函数 $f (x)$ 和 $g (x)$ 在区间 $A$ 上都是增(减)函数, 那么 $f (x) \pm g (x)$ 也是增(减)函数.
若两个正直函数 $f (x)$ 和 $g (x)$ 在区间 $A$ 上是增(减)函数, 那么函数 $f (x) \cdot g (x)$ 是增(减)函数.
若两个负直函数 $f (x)$ 和 $g (x)$ 在区间 $A$ 上是增(减)函数, 那么函数 $f (x) \cdot g (x)$ 是减(增)函数.

复合函数的单调性: 若函数 $f (x)$ 和 $g (x)$ 为单调函数, 那么函数 $f \circ g (x)$ 也是单调函数, 并且其单调性满足同增异减的规则.

性质中会出现很多题型.