ch01 向量引论

介绍两个重要的计算:

• $\mathit{v}+\mathit{w}$, 两个向量的加法.
• $c\mathit{v}$, 数字与向量相乘, 又称为数乘.
• 结合两个运算就有: $c\mathit{v}+d\mathit{w}$, 将其称为向量 $\mathit{v}$ 与 $\mathit{w}$ 的线性组合.

$c\mathit{v}$ 表示的向量都在一条直线上 (平行). 不在该条直线上的向量 $\mathit{w}$ 与该向量的线性组合: $c\mathit{v}+d\mathit{w}$ 生成整个二维平面. 但是四维空间中的四个向量 $\mathit{u}$, $\mathit{v}$, $\mathit{w}$, $\mathit{z}$ 的全部线性组合:

$$c\mathit{u}+d\mathit{v}+e\mathit{w}+f\mathit{z}$$

能否生成这个四维空间? 结论不一定成立 (什么样的可以生成整个空间算是后面套讨论的内容).

本书的主要思路:

1. 从基本的二维, 三维出发, 直观的展现线性代数的主要内容.
2. 然后将其对广到抽象的 $n$ 维空间中.

下面是本章的三个基本概念:

1. 向量的和, 与线性组合.
2. 两个向量的点积, 与向量的长度 $||\mathit{v}||$.
3. 矩阵 $A$, 线性方程组: $Ax=b$, 以及线性方程组的解: $\mathit{x}=A^{-1}b$.

1.1 向量与线性组合

两个单独的数字 $v_1$ 和 $v_2$ 构成一个二维向量 $\mathit{v}$ . ($n$ 个数字构成 $n$ 维向量).

书中采用列向量的形式书写: $\mathit{v}=\left[\begin{array}{c}{v}_1\\ v_2\end{array}\right]$, 其中 $v_1$, $v_2$ 是数字.

向量的加法: 对应分量相加, 得到一个新向量.

向量的减法: $\mathit{v}-\mathit{w}$, 对应分量相减, 得到一个新向量.

标量乘法, 又称为数乘. 将一个数字与向量相乘, 就是将这个数字与每一个分量相乘, 得到一个新向量.

$$2\mathit{v}=\left[\begin{array}{c}2v_1\\ 2v_2\end{array}\right]=\mathit{v}+\mathit{v}$$

其中数字 $2$ 就是标量.

零向量, 记为 $\mathbf{0}$. 注意不是数字 $0$, 它是一个向量, 只是每一个分量都是 $0$. $\mathit{v}$ 与 $-\mathit{v}$ 的和是零向量.

线性代数就是建立在向量的加法与标量乘法的基础上的.

线性组合

线性组合就是将向量进行标量乘法, 然后将其结果求和. 例如: $c\mathit{v}+d\mathit{w}$.

几个特殊的线性组合:

• $1\mathit{v}+1\mathit{w}$. 表示向量 $\mathit{v}$ 与向量 $\mathit{w}$ 的和.
• $1\mathit{v}-1\mathit{w}$. 表示向量 $\mathit{v}$ 与向量 $\mathit{w}$ 的差.
• $0\mathit{v}+0\mathit{w}$. 表示零向量. 实际上零向量可以写成任意个向量的线性组合, 系数都为 $0$ 即可.
• $c\mathit{v}+0w$. 表示与 $\mathit{v}$ 共线的向量.

然后书中介绍了二维向量的几何表示法 (自由向量).

几何上自由向量值关注向量本身的特征与具体位置无关, 自由向量相对于固定向量.

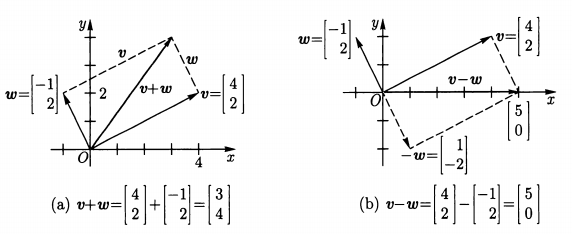
下图描述了向量加法与减法的含义:

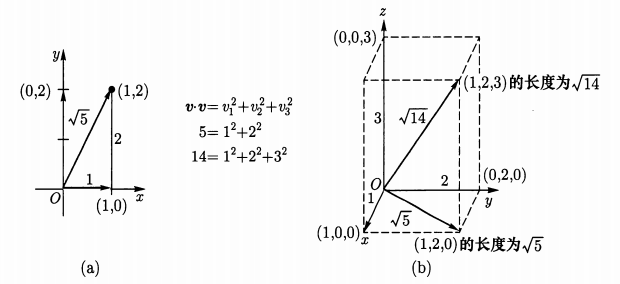
三维向量

借助于二维向量, 用三个分量 (标量) 构成一个三维向量. 然后介绍了列向量的表示, 以及几何含义.

本书中有一个重要的预设:

• 向量使用方括号来描述.
• 列向量为了节省排版空间, 会写成行的形式, 但是使用圆括号. 本质上是列向量.

所以: $[1,2,3]$ 与 $(1,2,3)$ 是不同的. $(1,2,3)$ 实际上是 $\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]$. 实际上 $[1,2,3]$ 是 $(1,2,3)$ 的转置.

所谓转置就是行列互换.

然后引入了三维向量的线性组合. 依旧是向量的数乘再求和.

几个重要问题

设有向量 $\mathit{u}$, $\mathit{v}$, $\mathit{w}$, 数字 $c$, $d$, $e$. 那么:

1. 形如 $c\mathit{u}$ 的全体线性组合是什么图形?
2. 形如 $c\mathit{u}+d\mathit{v}$ 的全体线性组合是什么图形?
3. 形如 $c\mathit{u}+d\mathit{v}+e\mathit{w}$ 的全体线性组合是什么图形?

实际上结果与三个向量 $\mathit{u}$, $\mathit{v}$, $\mathit{w}$ 之间的关系有关. 例如极端情况下, 如果三个向量都是零向量, 那么无论怎么线性组合, 结果就是零向量.

至于三个向量的不同关系的不同结果就与本课程的内容有关系了.

一个典型的结果是, 一条直线, 一个二维平面, 整个三维空间 (条线是三个向量线性无关).

要点回顾

1. 二维空间中的向量有两个分量. 推广一下, $n$ 维空间中的向量有 $n$ 个分量.
2. 向量的和, 与向量的数乘都是对向量的分量进行依次计算.
3. 三个向量的线性组合表示: $c\mathit{u}+d\mathit{v}+e\mathit{w}$ .
4. 三个向量的线性组合的几何含义: 直线, 平面, 空间.

范例解析

习题

1.2 长度与点积

主要内容:

• 向量的点积就是将各个分量对应相乘, 再求代数和.
• 点积为 0 的两个向量互相垂直.
• 向量与自己的点积的结果是向量长度的平方.
• 将向量 $\mathit{v}$ 的长度记为: $||\mathit{v}||$.
• 向量 $\mathit{v}$ 与 $\mathit{w}$ 夹角 $\theta$ 的余弦值为: $\cos \theta =\frac{\mathit{v}\cdot \mathit{w}}{||\mathit{v}||\cdot ||\mathit{w}||}$
• 由于 $|\cos \theta |\le 1$, 所以对任意的 $\mathit{v}$, $\mathit{w}$ 一定有: $|\mathit{v}\cdot \mathit{w}|\le ||\mathit{v}||\cdot ||\mathit{w}||$.

本章内容与几何具有密切联系 (主要是向量的长度, 与向量的夹角的余弦值).

内积 (点积) 的定义:

$$\begin{gathered} \mathrm{向}\mathrm{量}\mathit{v}=(v_1,v_2)\mathrm{与}\mathit{w}=(w_1,w_2)\mathrm{的}\mathrm{点}\mathrm{积}\mathrm{或}\mathrm{内}\mathrm{积}\mathrm{记}\mathrm{为}\mathit{v}\cdot \mathit{w},\mathrm{其}\mathrm{定}\mathrm{义}\mathrm{为}\mathrm{一}\mathrm{个}\mathrm{数}: \\ \mathit{v}\cdot \mathit{w}=v_1{w}_1+v_2{w}_2. \end{gathered}$$

示例

• 给出一个示例, 进行计算. 并通过案例介绍了互相垂直的向量, 点积为 $0$.
• 介绍了一个工程与科学的示例, 介绍了力矩的概念 (质量与坐标的乘积). 使用向量 $\mathit{m}$ 表示质量, 使用 $\mathit{s}$ 表示坐标, 保持平衡的条件是 $\mathit{m}\cdot \mathit{p}=0$.
• 让后给出一个商业示例, 利用向量类求解利润. 用向量 $\mathit{p}$ 表示商品的单价 (分量表示不同商品的单价), 使用 $\mathit{q}$ 表示商品数量 (分量表示不同商品的数量, 正负表示卖出和买入). 使用点积 $p\cdot q$ 表示收支. 作者还表示可以使用 Excel 来完成这个计算 (商业中 Excel 的适用很普遍).

长度与单位向量

向量 $\mathit{v}$ 的点积 $\mathit{v}\cdot \mathit{v}$ 的值等于长度的平方. 推广一下:

$$n\mathrm{维}\mathrm{向}\mathrm{量}\mathit{v}\mathrm{的}\mathrm{长}\mathrm{度}||\mathit{v}||\mathrm{等}\mathrm{于}\mathit{v}\cdot \mathit{v}\mathrm{的}\mathrm{算}\mathrm{术}\mathrm{平}\mathrm{方}\mathrm{根}.$$

然后利用图像和勾股定理进行了解释与证明.

单位向量: 长度为 $1$ 的向量为单位向量. 向量除以自身长度得到单位向量.

将与 $x$ 轴上的单位向量记为 $\mathit{i}$, 将 $y$ 轴上的单位向量记为 $\mathit{j}$.

在 $xy$ 平面上, 将单位向量 $\mathit{u}$ 与 $x$ 轴正方向的夹角记为 $\theta$, 那么这个单位向量可以记为 $(\cos \theta ,\sin \theta )$.

注意它是列向量.

• 当 $\theta =0$ 时, $\mathit{u}$ 就是 $\mathit{i}$.
• 当 $\theta =\pi /2$ 时, $\mathit{u}$ 就是 $\mathit{j}$.
• 显然 ${\sin }^2\theta +{\cos }^2\theta =1$.

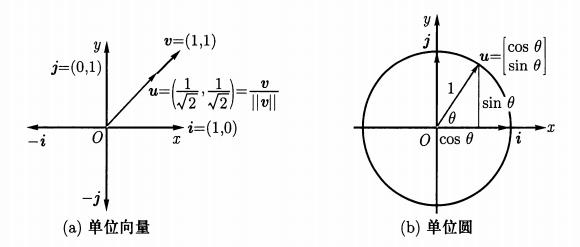
对任意的非零向量, 除以自身长度得到与当前向量方向相同的单位向量.

两个向量的夹角

点积为 $0$, 两个向量的夹角为 $\pi /2$.

零向量与任意向量都垂直.

两个单位向量 $\mathit{u}$, $\mathit{v}$ 的夹角记为 $\theta$, 那么 $\mathit{u}\cdot \mathit{v}=\cos \theta$. 并且 $|\mathit{u}\cdot \mathit{v}|\le 1$. 可推广至 $n$ 维向量.

下图是证明图解, 其中会涉及到三角函数公式. 细节略.

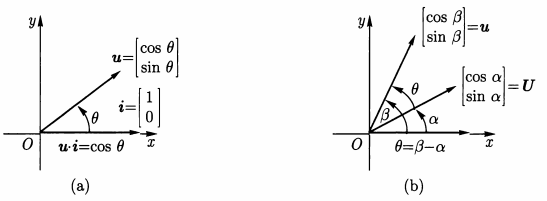
那么对与非单位向量怎么办? 向量除以自己的长度, 即得到单位向量, 那么有: 对与任意的向量 $\mathit{u}$, $\mathit{v}$, 记两向量的夹角为 $\theta$, 有:

$$\cos \theta =\frac{\mathit{v}\cdot \mathit{u}}{||\mathit{v}||||\mathit{u}||}$$

考虑到 $\cos \theta \le 1$, 得到施瓦茨不等式 (Schwarz):

$$|\mathit{v}\cdot \mathit{u}|\le ||\mathit{v}||||\mathit{u}||$$

全称是: 柯西-施瓦茨-布尼亚科夫斯基 (Cauchy-Schwarz-Buniakowsky) 不等式

三角不等式:

$$||\mathit{v}+\mathit{w}||\le ||\mathit{v}||+||\mathit{w}||$$

示例:

• 给出两个具体的向量, 计算两个向量夹角的余弦值.
• 利用施瓦茨不等式推导出 几何平均数 不大于 算数平均数.

关于计算机代数计算

Mathlab, Python, Julia 等都具备直接对向量分量计算的处理. 以 Matlab 为例:

• 输入 ' 可以实现转置.
• 输入分号, 表示结束, 开始计算.
• 直接输入表达式, 直接对向量分量进行计算.

v = [2 3 4]'; w = [1 1 1]'; u = 2 * v + 3 * w;

书写上两个向量的内积可以写成一个行向量左乘一个列向量来表示. 例如 $\mathit{v}=(1,2)$, $\mathit{w}=(3,4)$, 那么:

$$\mathit{v}\cdot \mathit{w}\mathrm{通}\mathrm{常}\mathrm{写}\mathrm{成}[1,2]\left[\begin{array}{c}3\\ 4\end{array}\right]$$

或写成 v' * v.

Matlab 中计算向量长度使用 norm(v), 也就是 sqrt(v' * v).

利用反三角函数 acos 可以利用向量求夹角:

cosine = v' * w / (norm(v) * norm(w))
angle = acos(cosine)

可以创建 M 文件, 将函数定义其中使用.

python 应该是基于 Numpy, Julia 暂时不清楚.

要点回顾

1. 点积的计算方法.
2. 获得单位向量, 以及向量长度的计算方法.
3. 向量垂直的判断.
4. 向量夹角的余弦值的计算方法, 以及施瓦茨不等式.

范例解析

习题

1.3 矩阵

主要内容

• 通常矩阵是一个 $m$ 行, $n$ 列的数字阵列, 表示上用方括号括起来.
• $A\mathit{x}$ 是矩阵 $A$ 和列向量 $\mathit{x}$ 的一个线性组合.
• 矩阵乘法的表示.
• 线性方程组的矩阵表示.
• $Ax=b$ 有解的条件.

本书中引入矩阵的方式比较特殊, 同时对矩阵乘法的引入也比较自然.

首先定义三个向量:

$$\mathit{u}=\left[\begin{array}{c}1\\ -1\\ 0\end{array}\right],\mathit{v}=\left[\begin{array}{c}0\\ 1\\ -1\end{array}\right],\mathit{w}=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right].$$

矩阵 $A$ 可以看成有这三个列向量并排得到的结果, 即: $A=[\mathit{u},\mathit{v},\mathit{w}]$. 可以写成:

$$A=\left[\begin{array}{ccc}1& 0& 0\\ -1& 1& 0\\ 0& -1& 1\end{array}\right]$$

而三个向量的一个线性组合: $x_1\mathit{u}+x_2\mathit{v}+x_3\mathit{w}$ 是:

$$x_1\left[\begin{array}{c}1\\ -1\\ 0\end{array}\right]+x_2\left[\begin{array}{c}0\\ 1\\ -1\end{array}\right]+x_3\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]=\left[\begin{array}{c}{x}_1\\ x_2-x_1\\ x_3-x_2\end{array}\right]$$

该线性组合可以看成矩阵 $A$ 左乘向量 $(x_1,x_2,x_3)$ 的结果:

$$A\mathit{x}=\left[\begin{array}{ccc}1& 0& 0\\ -1& 1& 0\\ 0& -1& 1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}{x}_1\\ x_2-x_1\\ x_3-x_2\end{array}\right]$$

形式上定义了矩阵乘法的规则: 左矩阵第 $i$ 行的元素, 与右矩阵的第 $j$ 列的元素, 依次相乘的代数和, 作为新矩阵的第 $i$ 行, 第 $j$ 列的元素.

所以 矩阵 $A$ 作用于向量 $\mathit{x}$, 所得的结果 $A\mathit{x}$ 是矩阵 $A$ 所有列向量的线性组合, 记为 $\mathit{b}$. 即有: $A\mathit{x}=\mathit{b}$.

由于 $A\mathit{x}$ 的结果是 $\mathit{x}$ 的差分 (第一项可以看成 $x_1-0$), 将矩阵 $A$ 称为差分矩阵.

由此可以构造一个 $4\times 4$ 的差分矩阵:

$$\left[\begin{array}{cccc}1& 0& 0& 0\\ -1& 1& 0& 0\\ 0& -1& 1& 0\\ 0& 0& -1& 1\end{array}\right]$$

Matlab 的一个 demo:

>> A = [1 0 0 0; -1 1 0 0; 0 -1 1 0; 0 0 -1 1];
>> A * [1, 2, 3, 4]'
> ans =

   1
   1
   1
   1
>>

另一个观点: 将 $A\mathit{x}$ 可以看成是 $A$ 的行向量与 $\mathit{x}$ 的点积构成的新向量:

$$A\mathit{x}=\left[\begin{array}{ccc}1& 0& 0\\ -1& 1& 0\\ 0& -1& 1\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}(1,0,0)\cdot (x_1,x_2,x_3)\\ (-1,1,0)\cdot (x_1,x_2,x_3)\\ (0,-1,1)\cdot (x_1,x_2,x_3)\end{array}\right]$$

线性方程组

上面的问题是给定 $\mathit{u}$, $\mathit{v}$, $\mathit{w}$, 以及 $x_1$, $x_2$, $x_3$, 怎么计算得到向量 $\mathit{b}$.

将问题调整一下, 给定向量 $\mathit{b}$, 向量 $\mathit{u}$, $\mathit{v}$, $\mathit{w}$ 怎么样的线性组合可以得到它. 这便有了线性方程组.

$$\{\begin{array}{ccccccc}{x}_1& & & & & =& b_1,\\ -x_1& +& x_2& & & =& b_2,\\ & & -x_2& +& x_3& =& b_3,\end{array}\mathrm{得}\mathrm{到}\mathrm{解}\mathrm{为}:\{\begin{array}{ccl}{x}_1& =& b_1,\\ x_2& =& b_1+b_2,\\ x_3& =& b_1+b_2+b_3,\end{array}$$

一般情况下线性方程组是比较难解的. 但是本例是一个特殊的三角形矩阵 (下三角形矩阵), 利用带入法, 从上之下可以依次解出来.

同时本例中的矩阵 $A$ 是可逆的, 存在逆矩阵 $A^{-1}$, 使得 $x=A^{-1}\mathit{b}$, 即为解.

至于怎么判断矩阵可逆, 以及怎么求逆矩阵. 暂时云中雾里.

逆矩阵

此处的一个结论: 如果 $\mathit{x}$ 的分量之差构成 $\mathit{b}$, 那么对 $\mathit{b}$ 的分量累加就能得到 $\mathit{x}$. 事实上这个累加矩阵就是原差分矩阵的逆矩阵.

$$\mathrm{解}Ax=b\mathrm{得}\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{l}{b}_1\\ b_1+b_2\\ b1+b_2+b_3\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 1& 1& 0\\ 1& 1& 1\end{array}\right]\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right]$$

至于怎么解, 这些结论什么的, 似乎暂时没有头绪. 但是这里案例说明

1. 每一个向量 $\mathit{b}$, 线性方程组 $A\mathit{x}=\mathit{b}$ 都存在一个解.
2. 利用矩阵 $A^{-1}$ 可以得到 $\mathit{x}=A^{-1}\mathit{b}$.

微积分注解

这里比较迷惑. 是一个类比吗? 或者是通过类比得到一个猜测?

可以将这些特殊的矩阵 (差分矩阵, 累加矩阵) 与微积分建立联系:

• 将向量 $\mathit{x}$ 看成一个函数 $x(t)$. 差分 $A\mathit{x}$ 变成导数 $\frac{\mathrm{d}x}{\mathrm{d}t}=b(t)$.
• 反过来, $A^{-1}\mathit{b}$ 中的累加就变成了对 $b(t)$ 的积分.

差分的和与导数的积分类似. 积分是微分的逆.

$$\mathrm{若}A\mathit{x}=\mathit{b},\mathrm{则}\mathit{x}=A^{-1}\mathit{b};\mathrm{若}\frac{\mathrm{d}x}{\mathrm{d}t}=b,\mathrm{则}x(t)={\int }_0^{t}b\mathrm{d}t.$$

但这个例子又给出结论差分不能等同于导数. 然后引出向前差分与向后差分:

• 向前差分: $x(t)-x(t-1)$
• 向后差分: $x(t)-x(t+1)$

最后得到中心差分: $((t-1{)}^2-(t+1{)}^2)/2=2t$.

书中提到在微积分中 中心差分不常见, 但这里巧合适用. 也许在数值计算中这个方法比较合适.

循环差分

书中说这里要介绍的是不可逆矩阵. 也许上面的差分也好, 中心差分也好, 只是为了说明逆矩阵可以计算线性方程组的解. 而这个类比也许只是一个开阔视野的联想.

使用三个新的向量 (更新 $\mathit{w}$):

$$\mathit{u}=\left[\begin{array}{r}1\\ -1\\ 0\end{array}\right],\mathit{v}=\left[\begin{array}{r}0\\ 1\\ -1\end{array}\right],{\mathit{w}}^{\mathbf{\ast }}=\left[\begin{array}{r}-1\\ 0\\ 1\end{array}\right].$$

来构造循环差分矩阵 $C$. 实际上这时的线性方程组没有唯一解. 要么无解, 要么无穷多解.

当 $C\mathit{x}=\mathbf{0}$ 时有无穷解, 解为 $(c,c,c)$ 的数. 对与 $C\mathit{x}=(1,3,5)$ 就无解.

$$C\mathit{x}=\left[\begin{array}{c}{x}_1-x_3\\ x_2-x_1\\ x_3-x_2\end{array}\right]=\left[\begin{array}{c}1\\ 3\\ 5\end{array}\right]$$

等式左边分量和为 $0$, 只有右边分量和也为 0 才有解.

几何上 $x_1\mathit{u}+x_2\mathit{v}+x_3{\mathit{w}}^{\mathbf{\ast }}$ 的全体线性组合都落在 $b_1+b_2+b_3=0$ 确定的平面上.

线性无关与线性相关

最后得到结论, 关键点是三个向量是否在一个平面内.

• 线性无关. $\mathit{w}$ 不在 $\mathit{u}$ 与 $\mathit{v}$ 生成的平面内.
• 线性相关. ${\mathit{w}}^{\mathbf{\ast }}$ 在 $\mathit{u}$ 与 $\mathit{v}$ 生成的平面内.

线性相关的另一个结论: ${\mathit{w}}^{\mathbf{\ast }}$ 是 $\mathit{u}$ 与 $\mathit{v}$ 的一个线性组合.

下面是线性代数的一个重要概念:

• 向量 $\mathit{u},\mathit{v},\mathit{w}$ 线性无关. 除了 $0\mathit{u}+0\mathit{v}+0\mathit{w}=\mathbf{0}$ 外, 没有任何其他线性组合可以生成零向量 $\mathbf{0}$.
• 向量 $\mathit{u},\mathit{v},{\mathit{w}}^{\mathbf{\ast }}$ 线性相关. 还有其他线性组合可以得到 $\mathbf{0}$, 例如: $\mathit{u}+\mathit{v}+{\mathit{w}}^{\mathbf{\ast }}=\mathbf{0}$.

用矩阵的语言来描述:

• $A$ 的列向量线性无关: $A\mathit{x}=\mathbf{0}$ 有唯一解, $A$ 是可逆矩阵.
• $C$ 的列向量线性相关: $C\mathit{x}=\mathbf{0}$ 有无穷多解, $C$ 是奇异矩阵.

若 $n$ 阶方阵的行列式为 0, 则该矩阵为奇异矩阵. 其特征:

• 不可逆. 非奇异矩阵 (行列式 $\ne 0$) 一定可逆.
• 秩小于 $n$. 非奇异矩阵是满秩的.
• 线性方程组无解或无穷多解.

要点回顾

1. 矩阵左乘向量得到线性组合.
2. 矩阵 $A$ 可逆, 则 $A\mathit{x}=\mathit{b}$ 的解是 $\mathit{x}=A^{-1}\mathit{b}$.
3. 循环矩阵 $C$ 没有逆矩阵, 它的三个列向量在同一个平面内. 这些列向量之和为 零向量, 从而 $C\mathit{x}=\mathbf{0}$ 有无穷多解.

范例解析

习题